<Derivation of the Classical Wave Equation>
Consider a vibrating string at a instant time:
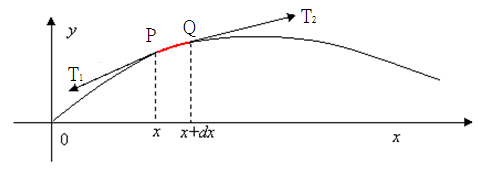
Focus on the red segment:
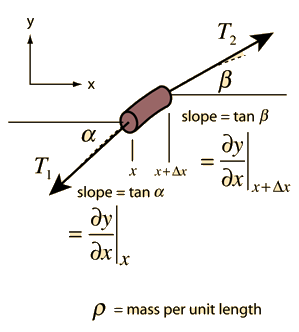
Assume that the string is homogeneous, and the mass of the string per unit length is r (a constant).
T1 & T2: tension acting on P & Q, and T1 & T2 are tangential to the curve of string.
Only vertical motion exists, that is, the horizontal components of the tensions at all points along the string must be equal.
Consider the horizontal part:

Consider the vertical force:
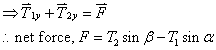
Upward motion is positive, “+”; Downward motion is negative, “-”.
According to Newton’s 2nd law, F = ma = rDx 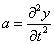
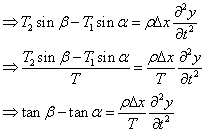
tanb and tana is the slope of curve at x & x+Dx.
that is,
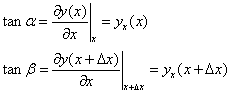
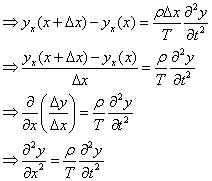
and let


v is the speed with which a disturbance propagates along a stretched string depends on the tension in the string and the linear mass density of the string.
<How to Solve it & Discussion>
Try separation of variables
y(x,t) = X(x)T(t)
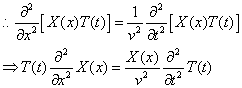
Multiply 1/y on both side
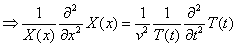
x and t are independent variables. This equation can only be valid if both sides are equal to a constant.
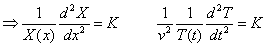
Note we have total not partial derivatives: linear, 2nd-order, and ordinary differential equation.
General solutions of have the form (see the below tables)
| Possible Solution | General Solution | ||
| K > 0 | ekx, e-kx | X(x) = A ekx + Be-kx | K = k2 |
| K < 0 | sin kx, cos kx | X(x) = C sin kx + D cos kx | K = -k2 |
Also for T(t) equation
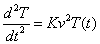
| K > 0 | T(t) = E evkt + F e-vkt |
| K < 0 | T(t) = G sin vkt + H cos vkt |
Now look at Boundary Conditions
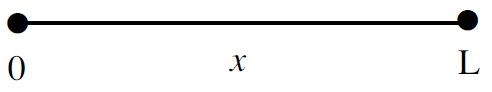
y(0,t) = 0
y(L,t) = 0
For K > 0, try to satisfy boundary conditions

so we should study the condition of〝K < 0 〞
For K < 0
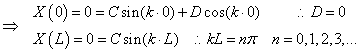
=> 〝quantization〞
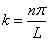
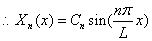
In the same way, we can solve T(t) when T(0) = 0.
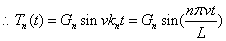
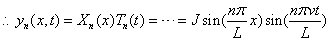
Now we choose the initial condition y = y0, that is J = y0
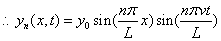
This is a set of solutions, one for each value of n. Each solution corresponds to a different standing wave. The differential equation, the boundary conditions, and the initial conditions have completely determined the set of wave functions.
The velocity is given by
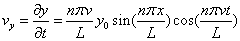
The velocity at t = 0
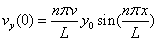
Our initial condition has specified the initial velocity. Instead of specifying the maximum amplitude we could have specified that the initial velocity is given by this function.
Typically for a standing wave, its wavelength (l) equals to 2L/n (n: number of standing wave), i.e. l is quantized.

The period t of our standing wave is the time required for the argument of the time factor sin(npvt/L) to change by 2p, so that

The frequency is quantized. It is directly proportional to the integer n, inversely proportional to the length of the string, directly proportional to the square root of the tension force, and inversely proportional to the square root of the mass per unit length.
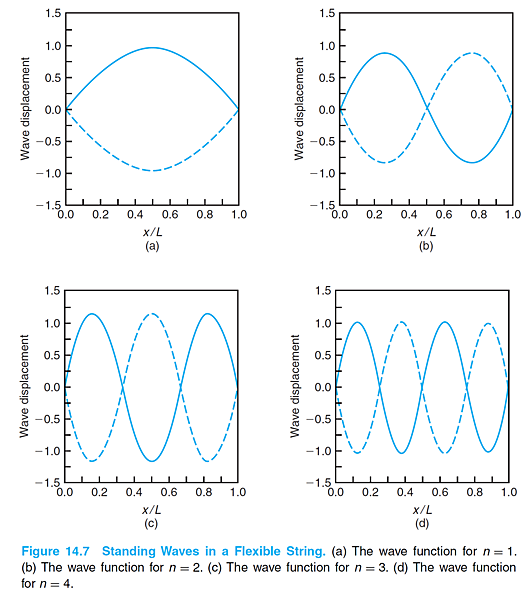
A string does not usually move as described by a single harmonic. A linear combination of harmonics can satisfy the wave equation:

The fact that a linear combination of solutions can be a solution to the wave equation is called the principle of superposition.

Reference:
1. Physical Chemistry 3rd Ed Robert G Mortimer
2. http://ocw.mit.edu/courses/chemistry/5-61-physical-chemistry-fall-2013/


 留言列表
留言列表